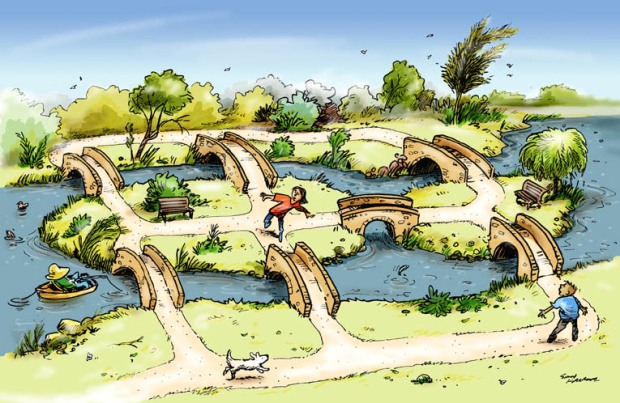
The city of Königsberg (capital of Prussia, now Kaliningrad, Russia) has the Pregel River running through the middle, with islands at the centre of the river connected by seven bridges. Is it possible to cross all of these bridges while only crossing them only once each?

If you try to solve this problem, you soon discover that it is incredibly difficult not to cross the same bridge twice. But it is difficult to tackle this problem in a brute force manner. To calculate all of the permutations in the order of bridges, you use 7! = 7 x 6 x 5 x 4 x 3 x 2 x 1 = 5040, meaning that there are 5040 possible arrangements of bridges. Then how can you prove if the problem is solvable or not?
The great mathematician Leonhard Euler, upon being asked to solve the problem, is reported to have said that the problem is impossible to solve on the spot. In 1735, he proved his answer by modelling the seven bridges of Königsberg in a diagram of four dots connected by lines (representing the bridges).

By using this model, the problem is converted into a “draw in one stroke” problem, which is also called a Euler walk to honour Euler’s contributions. Euler discovered many properties and laws regarding such problems. If a certain point is the starting point, then the line must first leave the point, then even if it comes back to the point, it must leave again. Ergo, the starting point must have an odd number of lines connected to it. The opposite applies to the ending point, where a line must enter the point, and if it leaves the point it must come back to it. Ergo, the ending point must also have an odd number of lines connected to it. In the case of a Euler walk, the starting and ending points are identical, so the number of lines is the sum of two odd numbers, making it an even number. Thus, to find out whether a picture can be drawn using one line, use the following laws:
- If there are no points of odd degree (odd number of lines), the starting and ending points are identical.
- If there are two points of odd degree, the starting and ending points are different.
- If there are one of more than two points of odd degree, it is impossible to draw using one stroke.
Thus, a Euler walk is only possible if there are 0 or 2 points of odd degree. Looking at the seven bridges of Königsberg problem, we can see that A is connected to 5 lines and B, C and D are connected to 3 lines each. As there are four points of odd degree, we have thus proved that it is impossible to draw a path that crosses all the bridges while not crossing any bridge more than once.