Imagine that you have won a strange lottery where they give you two options of payment: they can either pay you one million dollars up front, or they can pay you one cent on the first day, then double the amount you have every day for a month (i.e. 1 cent on day 1, 2 cents on day 2 etc.). Which would you choose?
It may seem obvious that the $1 million up front is far better than accumulating a few cents every day. But by the end of the month (day 31), you would actually have accumulated $5.37 million. How did this happen?
The secret to this extraordinary increase is the power of exponential growth. If you double a number constantly at a regular interval, it grows at a staggering rate. Let us look at the above example again.
On day 1, you have 1 cent. By day 10, you already have 2(10-1) = $5.12. Now we can see that instead of mere cents, we are gaining $5 in one day.
By day 15, you have $163.84. Now the doubling nets you another $163.
By day 20, you suddenly have $10,485.76.
We pass $1 million at day 28 where we have $1.34 million.
Day 29 you have $2.68 million and you can see how we end up with $5.37 million – over five times the amount we would have received compared to the first option.
This shows the sheer power of doubling. It is an important principle to grasp as we see exponential growth all around us in life. Nuclear chain reactions undergo exponential growth to power nuclear reactors. Positive feedback in speakers undergoes doubling amplification, resulting in the sharp screeching sounds. Compound interest follows exponential growth, allowing investments to give substantial returns over time (or result in crushing debt). Bacteria divide in two each time, resulting in a rapid population boom.

Understanding exponential growth also helps us make sense of scary situations such as pandemics. Viral infections are spread from one person to multiple people, represented by a basic reproduction number (R0). In the case of the COVID-19 (2019 coronavirus) pandemic, the R0 was between 2 and 3, meaning that left unchecked, the number of infected individuals would essentially double every few days.
Although this seems obvious, if you didn’t know about exponential growth, it would be terrifying to hear that one day you have 8 cases in a country, but in a fortnight, there are over 1000 cases, with each day presenting increasing numbers of newly infected patients. The media preys on this effect by providing anxiety-inducing headlines. But in reality, the headlines might as well read: “virus continues spreading in predictable exponential fashion“.
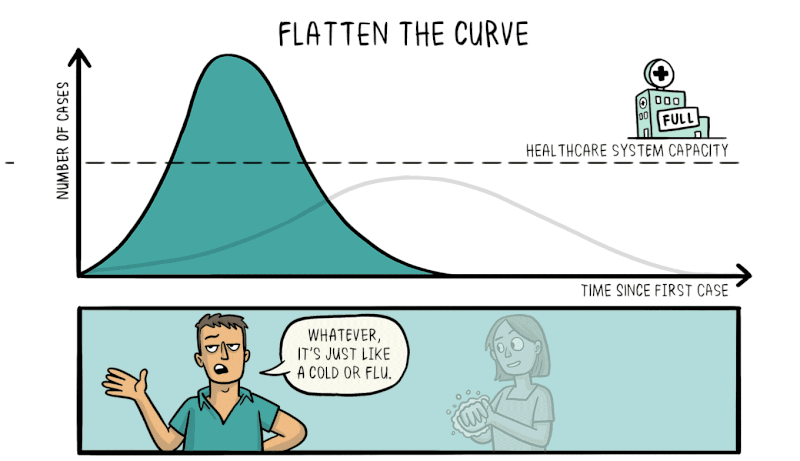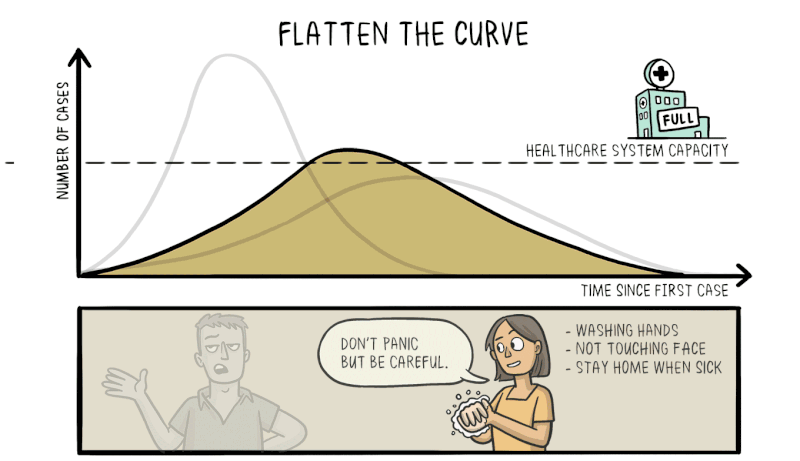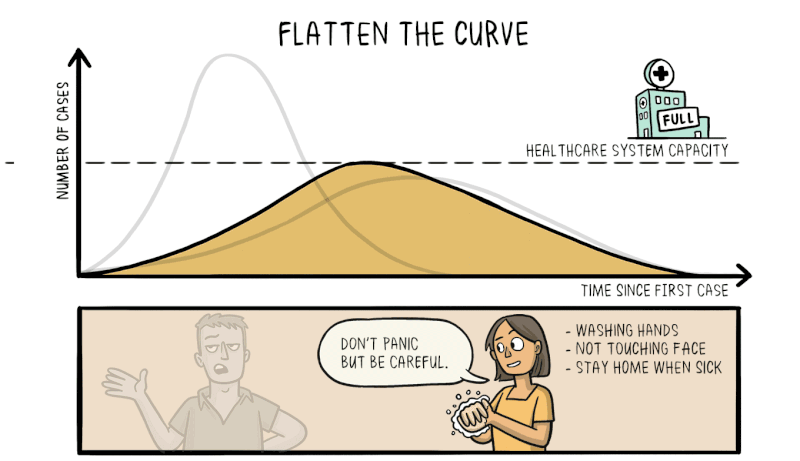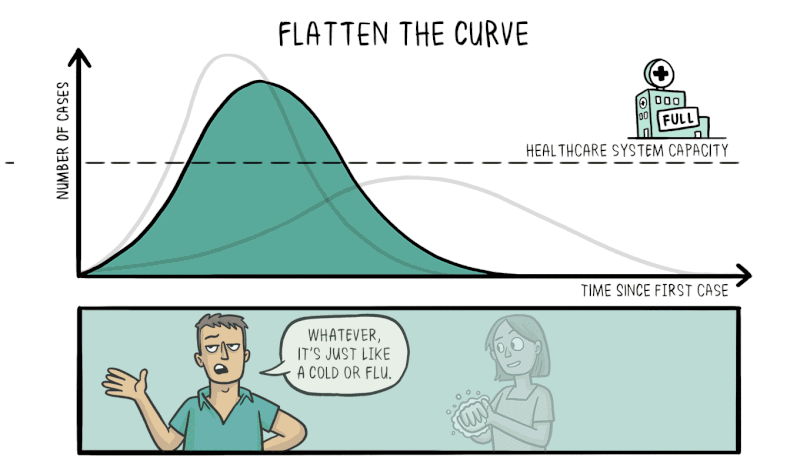
Another strength of knowing about exponential growth in a pandemic is that it lets us predict what would happen without any intervention. The number of cases would explode in a matter of weeks, resulting in catastrophic numbers of unwell people taken off the workforce, accompanied by mass casualties. Hospitals would be completely overrun, crippling the nation’s healthcare system and resulting in even more deaths as the infection runs rampant.
Therefore, efforts to reduce the spread of the virus through social distancing and effective quarantining are vital to reduce the rate of exponential growth, flattening the curve and making the number of cases more manageable for the healthcare system to deal with.